Esta es una transformación muy sencilla. Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.

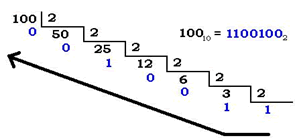
A continuación se obtiene el binario empezando por el último cociente y recolectando los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división precedidos por el último cociente, se les da la vuelta. Éste será el número binario que buscamos.

Ejemplo 1: Transformar el número decimal 362 en binario.

El método es muy simple:

	Convertir en binario el siguiente número: 362 División Resto Dato 362:2=181 0 0 181:2=90 1 1 90:2=45 0 0 45:2=22 1 1 22:2=11 0 0 11:2=5 1 1 5:2=2 1 1 2:2=1 0 0 1:2=0 1 1 El resultado es 101101010

 

 

 

 

 

 

A la hora de escribir el número se hace desde el último al primero.

Ejemplo 2: Transformar el número decimal 100 en binario.

Es importante mencionar que los subíndices que aparecen marcan el tipo de base que se utiliza en cada caso.

Ejemplo 3: Pasa el número 0,215 en base decimal a binario

En el caso en el que los números a trabajar sean fraccionarios o decimales, el proceso cambia levemente. La parte entera se opera igual que lo anterior, pero la parte fraccionaria se debe multiplicar por dos de forma que si el resultado obtenido tiene parte entera mayor o igual que uno se anota como 1, mientras si el resultado es menor que uno, se anota como cero. Así se opera sucesivamente hasta que no queda parte fraccionaria. Se colocan los números en base binaria en el orden en el que se obtienen.

Pasa el número 0,215 en base decimal a binario
División	Resultado	Dato a coger
0,59375*2	1,1875	1
0,1875*2	0,375	0
0,375*2	0,75	0
0,75*2	1,5	1
0,5*2	1	1
El resultado es 0,10011