Jednym z wielu działań, jakie można wykonać przy obserwacji rozwoju jaj w inkubatorze jest oszacowanie wielkości jaj umieszczonych wewnątrz inkubatora, ponieważ objętość może być przedstawiona jako elipsoida, a jajo jest strukturą złotego podziału. W tym celu, za pomocą programu Excel będziemy obliczać objętość jaja, z pomiarów osi wzdłużnej i poprzecznej (większej i mniejszej).

Wymiary i kształt jaja mogą być opisane w następujący sposób sumaryczny:

Parametr	Miara
Waga	60 g
Objętość	53 cm3
Średnia gęstość	1.132 g/cm3
Obwód wzdłużny	15.7 cm
Obwód szerokości	13.5 cm
Pole skorupki	68 cm2

Objętość jaja może być porównana do elipsoidy, wychodząc na to w następujący sposób:

Dwuwymiarowy kształt jaja można sformułować z połączenia dwóch elips jego mniejszych osi (zielona linia na rysunku). Trójwymiarowe jajo uzyskuje się przez obracanie dwuwymiarowego kształtu jaja wzdłuż osi większej (szara linia na rysunku). Pomiary szerokości i długości jaja pozwalają znaleźć jego objętość.

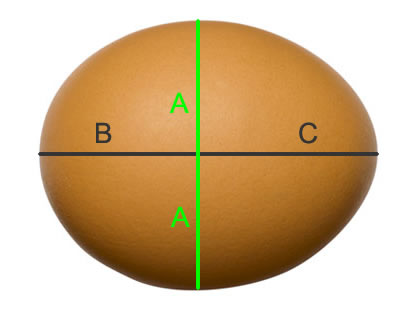
Szerokość jaja jest jego średnicą równikową. Połowa tej średnicy jest promieniem równikowym, który można nazwać A. Całkowita długość jaja jest jego średnicą biegunową. Odległością od równika jaja do najbliższego bieguna jest krótki promień biegunowy jaja; nazwijmy go B. Odległością od równika jaja do najdalszego bieguna jest długi promień biegunowy; zwany C.

Kształt jaja jest sumą dwóch połówek elipsoidy o różnych promieniach.

Objętość elipsoidy otrzymuje się za pomocą formuły:

 .

W naszym przypadku mamy dwie elipsoidy, zktórych jedna ma promień A, A i B, a druga ma promień A, A i C:

(1) R₁=A, R₂=A, R₃=B

(2) R₁=A, R₂=A, R₃=C

 

Końcowa formuła jest następująca:

 

Uczniowie mogą także skorzystać z kalkulatora jaja http://www.had2know.com/academics/egg-surface-area-volume-calculator.html

Biorąc pod uwagę, że średnia gęstość jaja kurzego wynosi od 1.055 do 1.104 gr/cm³, możemy ustalić objętość i co za tym idzie oszacować wagę każdego jaja. Dzięki tej informacji, spróbujemy ustalić korelację pomiędzy większą i mniejszą osią każdego jaja, używając suwmiarki, oraz objętość jaja. Gdy ta korelacja zostanie ustalona, możemy przejść do samego projektu (ponieważ nie można zważyć jaja), aby spróbować ustalić ewentualne szacunkowe wartości między promieniem osi z naszego eksperymentu in situ z objętościami inkubowanych jaj z pomiarów liniowych . W tym celu będziemy stosować prostą formułę rewolucji elipsoidy, którą to formułą będzie  gdzie R₁=(B+C) i R₂=A byłyby prostopadłymi promieniami jaja.