One of the many activities that can be performed with the observation of the development of an egg in an incubator is to estimate the volume of eggs placed inside the incubator, because the volume can be represented as an ellipsoid since the egg is a structure related to the golden ratio. For that, using Excel we will calculate, from measurements of the longitudinal and transversal axis (major and minor), the volume of the egg.

The dimensions and shape of an egg can be described in a summarized manner as:

Parameter	Measurement
Weight	60 g
Volume	53 cm3
Average density	1.132 g/cm3
Along circunfernce	15.7 cm
Circunference widthwise	13.5 cm
Shell area	68 cm2

The volume of an egg can be assimilated to an ellipsoid, leaving it in the following way:

The two-dimensional shape of an egg can be drawn by joining two ellipses at their minor axes (green line on the figure) A three-dimensional egg is obtained by rotating the two-dimensional egg shape along the major axis (gray line on the figure).  Measurements of the width and length of the egg allow finding its volume.

 

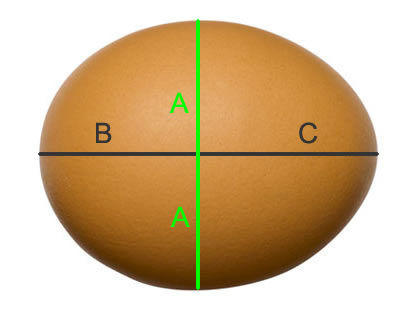
The width of an egg is its equatorial diameter. Half of this diameter is the equatorial radius, which you can call A. The total length of the egg is its polar diameter. The distance from the equator to the nearest pole is the short polar radius of the egg; call this number B. The distance from the egg's equator to the farthest pole is the long polar radius; call this number C.

The shape of an egg is sum of two halves of ellipsoids with different radius dimensions.

The volume of an ellipsoid is given by the formula: .

In our case we have two ellipsoids where one has radii of A, A, and B; the other has radii of A, A, and C:

(1)    R₁=A, R₂=A, R₃=B

(2)    R₁=A, R₂=A, R₃=C

The final formula is:

Students can also use the egg calculator http://www.had2know.com/academics/egg-surface-area-volume-calculator.html

Considering that the average density of hen eggs is between 1.055 and 1.104 gr/cm³, we can set a volume and consequently a weight estimate for each egg. With this information, we will try to establish a correlation between the major and minor axis of each egg, using a caliper, and the volume of the egg. Once this correlation is established, we can go to the project itself (since it can not weigh the eggs) to try to establish the possible estimates between the ratio of the axes of our in situ experiment with their volumes of incubated eggs from the linear measurements. For that, we will apply the simple formula of a revolution ellipsoid whose formula would be where R₁=(B+C) and R₂=A would be the egg orthogonal radii.