There are two basic ways of associating condensers in series and in parallel.

Series

Let us assume there are three capacitors with capacitance C1, C2 and C3. They are connected in series in the attached figure. If C is the capacitance of the equivalent capacitor.

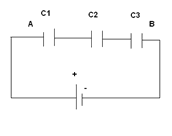
∆V₁ is the voltage drop between the terminals of the first

∆V₂ is the voltage drop between the terminals of the second

∆V₃ is the voltage drop between the terminals of the third

Then the following can be verified:

V_A -V_B = ∆V₁ + ∆V₂ + ∆V₃

When the first C1 terminal is charged, it will create an induced charge -Q in its second terminal. This charge will induce another of the same value and opposing sign +Q in C2, and so on.

Therefore, all capacitors have the same charge and this is equal to the total charge of the connection.

Parallel

Let us assume there are three capacitors with capacitance C1, C2 and C3. They are connected in parallel in the figure below.

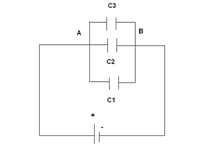
If Q1, Q2 and Q3 are the respective charges and ∆V₁, ∆V₂ and ∆V₃ the voltage drops between the terminals of each capacitor, then the following can be verified:

Q= Q1+Q2+Q3

V_A -V_B = ∆V₁ = ∆V₂ = ∆V₃

C= C1+C2+C3

With Q being the total charge of the connection and C the capacitance of the equivalent capacitor.

Other links about capacitors

Videos related to capacitors:

https://www.khanacademy.org/science/physics/electricity-and-magnetism/v/capacitance [EN]

http://www.youtube.com/watch?v=LW_mvJHyhrM [EN]

http://www.youtube.com/watch?v=4hqJSpf6F68 [EN]