This is a very simple transformation. The decimal system number is divided by 2, its result is divided by 2, and thus successively until the divided is smaller than the divisor, 2. This is, when the number to be divided is 1, the division is concluded.

Next, the reminders are ordered from the last to the first one. They are simply placed in reverse order as they appear in the division, they are turned around. This is the binary number that we are looking for.

Example 1: Transform the decimal number 362 into binary.

The method is very simple:

 

Convert to binary the following number: 362
Division	Reminder	Data
362:2=181	0	0
181:2=90	1	1
90:2=45	0	0
45:2=22	1	1
22:2=11	0	0
11:2=5	1	1
5:2=2	1	1
2:2=1	0	0
1:2=0	1	1
The result is 101101010

 

When you write the number it has to be done from the last to the first one.

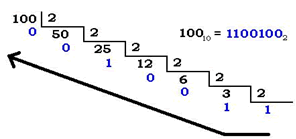
Example 2: Transform the decimal number 100 into binary.

 

 

It is important to mention that the sub-index that appear indicate the base type used in each case.

Example 3: Pass the decimal number 0,215 into binary

In the case that the numbers to work with are fractions or decimal, the process changes slightly. The integer part is operated the same as before, but the fractional-part has to be multiplied by 2, so that if the obtained result has integer part bigger or equal to 1 is written as 1, whilst if the result is less than 1, it is written as 0. Thus, it is operated until there is no fractional part left. The numbers in binary-base are placed in the order they are obtained.

Transform the decimal number 0,215 into binary
Division	Result	Data to collect
0,59375*2	1,1875	1
0,1875*2	0,375	0
0,375*2	0,75	0
0,75*2	1,5	1
0,5*2	1	1
The result is 0,10011