Gdy tylko wykres z tendencji linii zostanie uwidoczniony, jesteśmy w stanie stwierdzić, czy istnieje, czy też nie istnieje korelacja pomiędzy dwoma badanymi zmiennymi.

Doskonała korelacja ujemna. Zależność funkcyjna. Punkty "chmury" występują w linii prostej	r =-1
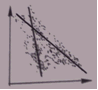Korelacja ujemna jest silniejsza jeśli zbliża się do -1 i słabsza jeśli zbliża się do 0. Zależność losowa..	-1<r<0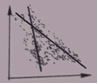
Zmienne nieskorelowane. Nie istnieje żaden związek miedzy zmiennymi. Niezależność losowa.	r=0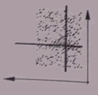
Korelacja dodatnia jest silniejsza im bardziej zbliża się do 1 i słabsza im bardziej zbliża się do 0. Zależność losowa.	0<r<1
Doskonała korelacja dodatnia. Zależność funkcyjna. Punkty “chmury” występują w linii prostej.	r=1

Źródła zewnętrzne:  https://www.khanacademy.org/math/probability/regression (EN)