To make a calculation with Excel, we first have to prepare the right table, as shown in the following figure, where we are going to include all data and the necessary calculations to obtain the corresponding correlation.

 

 

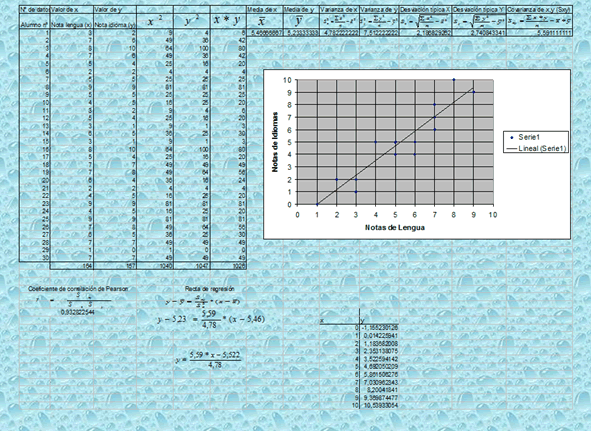
Next, we will establish all the procedures to be followed in each table column:

Column 1 - # data

In the first column (# data) we include the number of individuals or elements that take part in the sample, in our case 30 students.

Column 2 - Value of x (literature marking) and 3 - Value of y (marking of foreign language)

In these two columns the problems provided by the problem will be included, taking care of not making mistakes and that to each student the right marks are assigned per subject. In these tables, an additional cell is included where the sum of all data in a row is placed. For that, the range of data from the first to the last is marked by the following formula: =SUM(B4:B33) and =SUM(C4:C33), respectively.

Columns 4 and 5 - Value of x² and y²

In these two columns the data provided by the problem will be included, but in this case their square values. For that calculation, in the first cell of each column, the square value of the reference by the formula =B4^2 y =C4^2 will be included. Then, we will drag the cell until all the values are completed. In these tables, an additional cell is included where all the sum of the column values is placed. For that, mark the range of data from the first to the last one through the formula: =SUM(D4:D33) and =SUM(E4:E33) respectively.

Column 6 - Product xžy

In this column we will include the result of multiplying the data not provided by the problem. For that calculation, in cell F4 we will place, by means of the formula =B4*C4, a value which we will drag until all data is completed. In this cell we include an additional cell where the sum of all data of each column is included. For that, the range of data from the first to the last is marked by means of the formula: =SUM(F4:F33).

Columns 7 and  8 - Arithmetic mean of x and y

In these two columns we will include the data provided by the calculation of the arithmetic means of the problem data. For that, it is enough with dividing B34 by the number of students and, likewise, with C34, giving as result the arithmetic means of each subject, i.e. =B34/30 and =C34/34, respectively.

Columns 9 and 10 -Variance of x and y

In these two columns we will include the data provided by the calculation of the variance of the problem data. For that, the following operations will be performed =(D34/30) - G4^2 for the variance of x and =(E34/30) - H4^2 for the variance of y, respectively, giving as result the variances of each subject.

Columns 11 and 12 - Standard deviation of x and y

In these two columns we will include the data provided by the calculation of the standard deviations of the problem data. For that, we will carry out the following operations =I4^(1/2) for the standard deviation of x and =J4^(1/2) for the standard deviation of y, respectively, giving as result the standard deviations of each subject.

Columns 13 - Covariance of x , y

In this column we will include the data provided by the calculation of the covariance of x and y. For that, the following operation will be carried out =F34/30 -(G4*H4).